 1586
1586 2
2 1
1
მართკუთხედის დიაგონალების თვისების დასაბუთება სხვადასხვა ხერხით
ა) კოორდინატთა მეთოდის გამოყენება
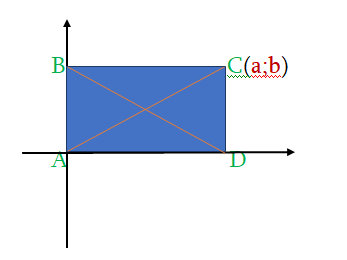 ვთქვათ, სიბრტყეზე საკოორდინატო სისტემა ისეა შერჩეული, რომ მისი სათავე ABCD მართკუთხედის A წვეროს ემთხვევა, AB და AD გვერდები კი საკოორდინატო ღერძებზე მდებარეობს; ვთქვათ, C წვეროს კოორდინატებია a და b; C(a;b)
ვთქვათ, სიბრტყეზე საკოორდინატო სისტემა ისეა შერჩეული, რომ მისი სათავე ABCD მართკუთხედის A წვეროს ემთხვევა, AB და AD გვერდები კი საკოორდინატო ღერძებზე მდებარეობს; ვთქვათ, C წვეროს კოორდინატებია a და b; C(a;b)
იპოვეთ მართკუთხედის სხვა წვეროების კოორდინატები
A(0;0)
B(b;0)
D(a;0)
იპოვეთ მართკუთხედის დიაგონალების სიგრძეები
M2(ერთი დიაგონალი) = CD2 + AD2
M=√(CD2 + AD2)
N2(მეორე დიაგონალი) = AB2 + AD2
N=√(AB2 + AD2)
შეადარეთ მიღებული გამოსახულებები და ჩამოაყალიბეთ მართკუთხედის დიაგონალების თვისება მართკუთხედის დიაგონალები ერთმანეთის ტოლია, რადგან
AB2 = CD2 და AD2 = AD2
ბ)სამკუთხედის ტოლობის გამოყენება
განიხილეთ ABD და DCA მართკუთხა სამკუთხედები
 სამკუთხედი ABD
სამკუთხედი ABD
სამკუთხედი DCA
დაასაბუთეთ, რომ ეს სამკუთხედები ტოლია
ეს სამკუთხედები ტოლია რადგან, ჩვენ უკვე დავასკვენით რომ მართკუთხედის დიაგონალები ტოლია, ასევე კუთხე Aუდრის კუთხე D-ს და ორივე სამკუთხედს აქვთ ერთი საერთო კათეტი.
სამკუთხედების ტოლობის რა ნიშანი გამოიყენეთ?
გამოვიყენეთ სამკუთხედის ტოლობის პირველინიშანი: თუ ერთი სამკუთხედის ორი გვერდი და მათ შორის მდებარე კუთხე ტოლია მეორე სამკუთხედის 2 გვერდის და მათ შორის მდებარე კუთხის, მაშინ ეს სამკუთხედები ტოლია.
რა შეიძლება ვთქვათ ამ ტოლი სამკუთხედების ჰიპოტენუზების შესახებ?
როგორც ზემოთ აღვნიშნეთ მათი ჰიპოტენუზები ტოლია.
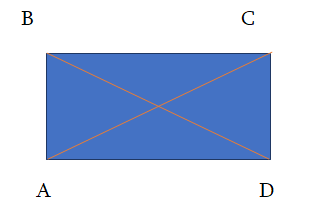 მართკუთხედის დიაგონალები ტოლია
მართკუთხედის დიაგონალები ტოლია
დაასაბუთეთ: თუ პარალელოგრამის დიაგონალები ტოლია, მაშინ ის მართკუთხედია
მოცემულია სამკუთხედი ABD და ACD
AB=CD
AC=BD
AD არის საერთო კათეტი
< ABD = < ACD მესამე ნიშნით
< BDA = < CDA
< A= < B =
წყარო
სახელმძღვანელო
მოიწონეთ გვერდი
დამატებული კომენტარები
სახელი: ლ
დრო: 2020-02-12
კომენტარი: დიდი მადლობა, რა მაგარია



